Hierarchical Navigable Small World (HNSW) in PHP

Ovvero: Come trovare un ago in un pagliaio senza controllare tutta la paglia

Nel precedente articolo abbiamo visto come i vettori possano aiutare a trovare l'informazione giusta semplicemente descrivendo il concetto che vogliamo trovare.

Abbiamo usato la Cosine Similarity per confrontare la nostra richiesta con tutti i documenti disponibili, scorrendoli uno per uno fino a trovare quelli con similitudine maggiore. Questo approccio funziona? Sì. È veloce? Insomma....

Immagina se un bibliotecario, per trovare il tuo libro, dovesse leggere i titoli di tutti i 10 milioni di volumi di una Biblioteca Nazionale. Anche se impiegasse un millisecondo a libro, ci metterebbe ore. Questo è il problema della ricerca lineare ($O(N)$).

Per risolvere questo problema introduciamo un concetto che trasformerà quella ricerca di ore in millisecondi: HNSW (Hierarchical Navigable Small World).

Piccoli mondi e autostrade

Facciamo una analogia per intuire meglio la soluzione che HNSW ci propone: Come facciamo a trovare un punto specifico in una città enorme se proveniamo da molto lontano e non conosciamo la direzione?

Semplice: nella vita reale usiamo una gerarchia di strade. Ovvero partiamo da una visione "ampia" della mappa e successivamente "zoomiamo" verso il punto di interesse. Volendolo esprimere con un algoritmo faremmo:

Prendiamo l'autostrada per avvicinarci alla regione.
Usciamo sulla statale per arrivare alla città.
Prendiamo le vie principali per il quartiere.
Infine usiamo le stradine per trovare il civico.

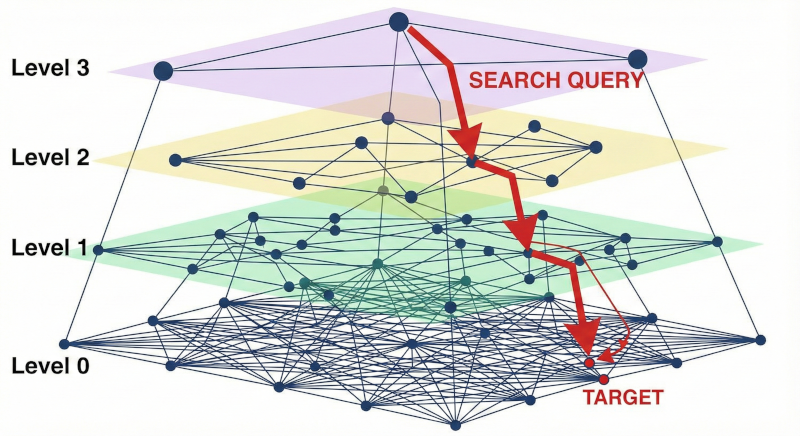
HNSW fa esattamente questo con i dati. Costruisce una struttura a strati (Layers) dove i livelli più alti sono come le autostrade (pochi punti, collegamenti lunghi) e i livelli bassi sono le strade di quartiere (tutti i punti, collegamenti corti).

Il codice

Analizziamo come implementare questa logica in PHP. Il codice che esamineremo proviene dal progetto open source Vektor, una piccolo servizio che ho realizzato che permette di eseguire la ricerca vettoriale nativa in PHP.

Nota tecnica: Oltre a $ef, esiste un parametro cruciale chiamato $M. Immaginatelo come il numero massimo di strade che possono partire da un incrocio. Più alto è $M, più la città è connessa, ma più memoria occuperà la nostra mappa.

La discesa fino al Livello 0

La logica principale è nel metodo search, che vediamo di seguito. Immagina di guardare una mappa satellitare e fare zoom progressivi. Partiamo dalla visione globale (i nodi del livello più alto).

public function search(array $queryVector, int $k, int $ef): array
{
    // Iniziamo dal livello più alto (es. Livello 3)
    $entryPoint = $this->readHeader();

    // Calcoliamo la distanza iniziale, cioè confrontiamo l'oggetto di Livello 3 con il target di ricerca
    $currObj = $entryPoint;
    $currDist = Math::cosineSimilarity($queryVector, $this->getVector($currObj));

    // Ora scendiamo progressivamente dai livelli alti fino al livello 1
    // Il ciclo for parte dal livello massimo e si ripete finché non raggiungiamo Livello 1
    for ($lc = $maxLevel; $lc >= 1; $lc--) {

        // Navighiamo nel livello corrente finché non troviamo il punto più vicino
        while (true) {
            $changed = false;

            // Leggiamo i vicini del nodo corrente in questo livello
            $node = $this->readNode($currObj);
            $neighbors = $node['connections'][$lc] ?? [];

            // Cerchiamo se c'è un vicino che è PIÙ VICINO al nostro target
            foreach ($neighbors as $neighborId) {
                $dist = Math::cosineSimilarity($queryVector, $this->getVector($neighborId));
                if ($dist > $currDist) {
                    $currDist = $dist;
                    $currObj = $neighborId;
                    $changed = true; // Abbiamo trovato un punto migliore!
                }
            }

            // Se non ci sono stati cambiamenti nella scelta del nodo migliore,
            // significa che siamo già nel punto più vicino possibile in questo 
            // livello e quindi possiamo "scendere" al livello inferiore
            if (!$changed) break;
        }

        // Ora $currObj è valorizzato con il punto di partenza per il livello inferiore ($lc - 1)
    }

    // Alla fine del for ci troveremo nel Livello 0 e $currObj conterrà il punto più vicino!
}

Questo ciclo è l'equivalente di identificare la zona di interesse dall'alto, spostarsi verso il punto più vicino alla destinazione, e poi aumentare il dettaglio. Ripetiamo finché non siamo al livello di dettaglio massimo (Livello 1).

La ricerca di precisione (Level 0)

Una volta arrivati al Livello 0, dove risiedono tutti i dati, non ci basta più un solo punto. Vogliamo i K risultati migliori. Qui entra in gioco il parametro $ef (Construction/Search Size).

$ef è la dimensione della nostra "lista candidati". Più il numero è alto, più nodi valutiamo, più precisa (e lenta) sarà la ricerca.

Il metodo searchLayer adotta un approccio Greedy: a ogni passo l'algoritmo effettua la scelta localmente ottima, muovendosi verso il vicino che massimizza la similitudine con la query. Invece di esplorare ogni possibile percorso, l'algoritmo "segue il gradiente" verso il target. La Coda di Priorità gestisce questo processo, permettendoci di esplorare prima i nodi più promettenti e di interrompere la ricerca non appena i nuovi candidati smettono di migliorare la nostra lista dei risultati migliori ($ef$).

public function searchLayer(int $entryPoint, array $queryVector, int $ef, int $level, ?int $k = null): array
{
    $visited = [$entryPoint => true];
    $candidates = new SplPriorityQueue(); // I nodi promettenti da esplorare

    $winners = [$entryPoint => $entrySim]; // I migliori risultati trovati finora (Winner list)

    while (!$candidates->isEmpty()) {
        $c = $candidates->extract(); // Prendi il miglior candidato

        // Se il miglior candidato è peggiore del peggiore dei nostri "vincitori" attuali
        // e abbiamo già riempito la lista ($ef), possiamo fermarci.
        // È inutile esplorare oltre, ci stiamo allontanando.
        if ($cSim < $worstSim && count($winners) >= $ef) {
            break;
        }

        // Esploriamo i vicini del candidato
        $node = $this->readNode($c);
        $neighbors = $node['connections'][$level] ?? [];

        foreach ($neighbors as $neighborId) {
            if (!isset($visited[$neighborId])) {
                $visited[$neighborId] = true;

                // Per ogni vicino calcoliamo la sua similitudine con la query target
                $sim = Math::cosineSimilarity($queryVector, $this->getVector($neighborId));

                // Se questo vicino è promettente, lo aggiungiamo ai candidati
                if ($sim > $worstSim || count($winners) < $ef) {
                    $candidates->insert($neighborId, $sim);
                    $winners[$neighborId] = $sim;

                    // Manteniamo la lista W di dimensione fissa $ef
                    if (count($winners) > $ef) {
                        asort($winners);
                        $idToRemove = array_key_first($winners); // Rimuovi il peggiore
                        unset($winners[$idToRemove]);

                        // Aggiorniamo la soglia di "peggiore accettabile"
                        asort($winners);
                        $worstSim = $winners[array_key_first($winners)];
                    }
                }
            }
        }
    }

    // ... ritorna i top K elementi dall'elenco dei $winners ...
}

Perché è veloce?

Torniamo all'esempio della biblioteca.

Nella Ricerca Lineare il bibliotecario controlla ogni libro. $O(N)$ operazioni.
Nella HNSW il bibliotecario guarda il reparto "Scienze" (Livello 2), poi va allo scaffale "Astronomia" (Livello 1), e infine controlla solo i 50 libri di quello scaffale (Livello 0). $O(\log N)$ operazioni.

Su un dataset di 1 milione di oggetti, invece di fare 1.000.000 di confronti, ne facciamo magari solo 500 o 1.000. È una differenza di ordini di grandezza.

Costruire la mappa

Finora abbiamo dato per scontato che queste "autostrade" e "strade di quartiere" esistano già. Ma come vengono costruite? La genialità di HNSW sta nel fatto che la mappa viene disegnata dinamicamente, un punto alla volta.

Quando dobbiamo inserire un nuovo dato (un vettore) nel nostro indice, dobbiamo decidere due cose:

In che zona si trova? (Livello massimo)
Chi sono i suoi vicini?

Per la prima domanda, HNSW si affida al caso. È come lanciare una moneta (o più tecnicamente, usare una distribuzione di probabilità esponenziale). La maggior parte dei punti finirà al Livello 0 (il quartiere residenziale). Alcuni fortunati vinceranno un "biglietto" per il Livello 1 (le statali). Pochissimi "eletti" arriveranno ai livelli più alti (le autostrade). Questo garantisce che i livelli superiori rimangano sgombri e veloci da percorrere.

Per la seconda domanda, invece, usiamo la ricerca vista in precedenza per fare anche l'inserimento.

Se il nostro nuovo punto è stato assegnato al Livello 1:

Partiamo dal livello più alto in assoluto (es. Livello 3).
Cerchiamo il punto più vicino al nostro nuovo arrivato (usando la logica del searchLayer vista prima).
Scendiamo al livello sotto e ripetiamo, finché non arriviamo al livello assegnato (Livello 1).
Qui ci fermiamo e colleghiamo il nuovo punto ai suoi vicini più prossimi (in base al parametro $M, il numero massimo di connessioni).

In pratica, ogni nuovo cittadino che arriva in città chiede indicazioni per trovare la sua zona, e una volta arrivato, stringe amicizia con i vicini più simili a lui. Se un vicino ha troppi amici, taglia i ponti con quello meno simile per fare posto al nuovo arrivato. È questo processo di selezione naturale delle connessioni che mantiene il grafo efficiente e navigabile.

Conclusione

Implementare HNSW da zero è un esercizio fondamentale per capire come funzionano i moderni database vettoriali come Qdrant o Pinecone. Non stiamo solo "cercando dati", stiamo navigando in uno spazio multidimensionale usando scorciatoie probabilistiche.

Questi algoritmi sono la base dei moderni sistemi di raccomandazione ("Utenti che hanno comprato questo hanno visto anche....") e dei sistemi di RAG (Retrieval Augmented Generation) per le intelligenze artificiali, permettendo di trovare il contesto rilevante in frazioni di secondo.

Se volete approfondire l'implementazione completa, date un'occhiata al repository di Vektor https://github.com/centamiv/vektor su GitHub.